Challenges of Engineer Autonomic Behaviors
A well recognized research challenge for future large-scale pervasive computing scenarios relates to the need of enforcing autonomic, self-managing and self-adaptive, behaviour, both at the level of the infrastructure and at that of its services.
Indeed, the increasing decentralization and dynamics of the current and emerging ICT scenarios (a variety of highly-distributed devices of an ephemeral and/or mobile nature, with users and developers capable of injecting new components and services at any time) make it impossible for developers and system managers to stay in the control loop and directly intervene in the system for configuration and maintenance activities (e.g., for configuring or personalizing new distributed devices or services, for fixing problems in existing devices and services, or for optimizing resource exploitation).
Accordingly, in the past few years, a large number of research proposals have been made, at both the infrastructural and service levels, to promote autonomic and adaptive behaviour in pervasive computing systems. However, in our opinion, most of the current proposals suffer from several limitations when dived in future scenarios.
First, a number of approaches propose “add-ons” to be integrated in existing frameworks as, e.g., in the case of those autonomic computing approach “à la IBM”, suggesting coupling sophisticated control loops to existing systems to support self-management. The result is often in an increased complexity of current frameworks, which definitely does not suit the characteristics and the need for lightness of pervasive scenarios.
Second, a number of other proposals suggest relying on light-weight and fully decentralized approaches, typically inspired by natural phenomena of self-organization and self-adaptation. However, most of these exploit the natural inspiration only for the implementation of specific algorithmic solutions or for realizing specific distributed services, either at the infrastructural or at the user level, rather than for attacking the issue of autonomic self-adaptation in a comprehensive way.
Third, and although an increasing number of researchers focuses on the social aspects of pervasive computing and on the provisioning of innovative social services, they do not properly account for the social level as an indistinguishable dimension of the overall pervasive computing fabric. That is, they do not account for the fact that users, other than simply consumers or producers of services, are de facto devices of the overall infrastructure, and contribute to it via human sensing, actuating, and computing capabilities, other than via an inherent strive for adaptation.
Based on the above considerations, our belief is that – rather than looking for one-of solutions to specific adaptation problems from specific limited viewpoints – there is need to deeply rethink the modelling and architecting of modern pervasive systems. As challenging as this can be, one should try to account in a foundational and holistic way for the overall complex needs of adaptation and autonomic behaviour of future pervasive computing systems. The final goal should be that of making such systems inherently capable of autonomic self-management and adaptation at the collective level, and having the distinction between infrastructural, services, and social levels, blur or vanish completely.
The achievement of the outlined broad goal calls for facing a number of specific challenging research issues, necessary to compose the global picture. These may include, among the others:
- Supporting Comprehensive Self-awareness. While the need for situation-awareness is already a recognized issue in pervasive computing, future scenarios will require autonomous adaptation activities to be driven by more comprehensive levels of awareness than traditionally enforced in context-aware computing models, where it is typically up to each component to access and digest the information it needs to take adaptation decisions. Such awareness models should encompass situations occurring at the many different levels of the system, as well as the strict locality of components, and be eventually able to provide components of the pervasive computing infrastructure with expressive and compact representations of complex multi-faceted situations, so as to effectively drive each and every activity of the components in a collectively coordinated way.
- Reconciling Top-Down vs Bottom Up Approaches. Along with the traditional “top-down” approaches to the engineering of pervasive computing systems, in which specific functionalities or behaviour are achieved by explicit design, “bottom-up” approaches are being proposed and adopted too (as we have already anticipated), to achieve functionalities via spontaneous self-organization, as it happens in natural systems. Most likely, both approaches will coexist in future pervasive computing scenarios, the former applied to the engineering of specific local functionalities, the latter applied to the engineering of large-scale behaviours (or simply emerge as a natural collective phenomena of the system). Thus, there will be need to understand the trade-offs between the power of top-down adaptation and bottom-up one, also by studying how the two approaches can coexist and possibly conflict in future systems, and possibly contributing in smoothing the tension between the two.
- Enforcing Decentralized Control. In large-scale systems, we should never forget that the existence and exploitation of phenomena of collective adaptation must necessarily come along with models and tools making it possible to control “by design” the overall behaviour of the pervasive systems and its sub-parts. Clearly, due to the inherent decentralization of the systems, such control tools too should make it possibly to direct the behaviours of the system in a decentralized way, and should be coupled by means to “measure” such behaviours in order to understand if the control is effective. The issue of defining sound measures for future pervasive computing scenarios can define in itself a challenging research area, given the size of the target scenario and the many – and often quite ill-defined – purposes it has to concurrently serve.
The need for laying out brand new foundations for the modelling and architecting of autonomic and self-adaptive pervasive computing systems, opens up a large number of fascinating and challenging research questions. In the ASCENS project, we are trying to understand how it is possible to identify a sound set of self-aware adaptation patterns for ensemble, and how such patterns can be used for engineering both top-down and bottom-up adaptation schemes, other than for enforcing in a decentralized way control over the global behaviour of ensembles.
In any case, the short list of challenges that we have provided above and that we are currently tackling in ASCENS is far from being exhaustive. For instance, it does not account for the many inter-disciplinary issues that the understanding of large-scale socio-technical organisms (as future pervasive computing systems will be) and their collective adaptive behaviours involve , calling from exploiting the modern lessons of applied psychology, sociology, social anthropology, and macro-economy, other than those of systemic biology, ecology and complexity science. Plenty of room for additional projects to complement ASCENS!
Formal Methods for Computer System Engineering
[This post is the continuation of "What can Formal Methods do?", which I posted to this blog on Jan. 31, 2012. In that post I tried to motivate the need of Formal Methods (FMs) in Computer System Engineering (SE). In the present post I briefly sketch some of the basic concepts and notions in the area of FMs for concurrent systems]
Let me start by recalling the quotation I made in my previous post: “All engineering disciplines make progress by employing mathematically based notations and methods.” [Jon00]. C. Jones continues as follows: “Research on `formal methods' follows this model and attempts to identify and develop mathematical approaches that can contribute to the task of creating computer systems”. This statement is complemented by what W. Thomas writes in the same book, i.e. FMs “Attempt to provide the (software) engineer with concepts and techniques as thinking tools, which are clean, adequate, and convenient, to support him (or her) in describing, reasoning about, and constructing complex software and hardware systems” [Tho00].
In a nutshell, we can say the FMs for Computer System Engineering (SE) find their roots in Theoretical Computer Science (TCS) and in Mathematical Logics (ML) but they differ from both TCS and ML in their primary goal, which is pragmatic rather than foundational with emphasis on construction, automatic (often `push button’) software tool support, rather then on fundamental questions like computability of completeness (in the technical sense) of theories. In the following I’ll show a simple example of logic/mathematics notions and structures used in FMs for SE. For space reasons I’ll consider only the case of abstractions for distributed, actually concurrent, systems, i.e. systems composed of (very) many components, where each component (usually) performs (very) simple tasks (often sequential), but the interaction among components is usually complex, difficult to understand, non-deterministic, and subtle (due to race conditions, synchronization issues, dead-/live-locks, etc.). This choice does not mean (by no means!) that non-concurrent systems are easy to design or that the theory behind such systems is not interesting. Extremely important foundational work has been produced in the area of sequential computing, including the basics of computability theory, of operational and denotational semantics, formal program analysis and transformation, etc. The choice is mainly due to reasonable space limitations, to the focus of ASCENS as well as personal taste and competence.
Most mathematical structures used for modelling concurrent systems are variants of Labelled Transition Systems (LTSs). Often, such models are syntactically represented as terms of suitable Process Algebras (PAs, well ... PAs are, as the words themselves should suggest, much more than just languages for specifying models!). LTSs are state-transition structures, i.e. structures in which the behaviour of a system is modelled by means of a set of (global) states, which the system can be in, and a set of transitions, which describe how a system can move from which state to which one. What a state is depends on what the designer wants to model: states are not necessarily associated to specific information `per se’. This is a point where system designer ingenuity is crucial. A state could be associated to a specific set of voltages at the components of an electrical circuit, in which case a transition would correspond to a possible change in such values. I guess we can agree that such a modelling choice would probably bring to models with huge numbers of states and transitions! More realistically one could think of associating a different state to each specific set of values of variables and execution points of the software components of a distributed system at a given point in time, in which case a transition would correspond to the execution of a command. But a state could also correspond to a certain position of the parts of a robot that are relevant for a certain application, in which case transitions would model possible changes of position. At an even more abstract level of modelling, a state could simply represent whether a given shared resource is free or not, and a transition would model granting or refusing a request of usage of that resource. Regardless of the specific interpretation we assign to states and transitions, a state-transition structure is a mathematical structure as follows: (S, -->) where S is a non-empty set of states (usually finite or denumerable) and --> is a binary relation on S. It is often useful to associate labels to transitions, denoting specific actions of our system, so that a typical definition of a LTS is a triple (S, L, -->), where L is a non-empty transition label set and --> is a relation over S x L x S; again, notice that typically, no particular assumption needs to be made on the elements of L, their specific interpretation being left to the designer of the specific model; in some cases, instead, it might be more convenient do fix a specific structure of labels.
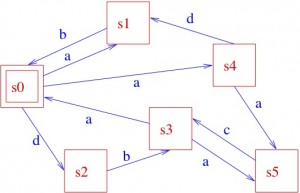
We can use graphical notations as well:
From the initial state s0, by executing action a, the system can get to state s1 or s4 (yes, some systems can be non-deterministic... ), while the execution of action d brings the system to state s2, and so on. You will also easily understand that the information captured by the above picture could very well be described textually, as follows:
where the notation x.P specifies that a transition labelled by x brings the system to (the) state (specified by) P, and an expression like P1 + P2 specifies a state that may behave like (specified by) P1 or (specified by) P2, so that it should now be easy to infer that the behaviour specified above for our system when being in state, say, s0 is indeed that prescribed by the LTS in the picture, and so on. In some cases, one might find it useful to label states, instead of transitions; the resulting structures, known as Kripke Structures [after the famous logician], form the basis for the semantics of modal logics, which temporal logics are a special case of and represent one of the most successful tools for the formal specification of system requirements. Of course, we sometimes find it useful to have both state and transition labels. As the above example might have suggested, one can model more and more complex behaviours by means of composing simpler ones, using operators like . and +. In fact, many more operators are commonly used, including parallel composition ones, by means of which one can put different LTSs together and study the overall behaviour when they execute “in parallel”. So, the game is again to have (1) a set of basic components and (2) ways for composing them. In fact, what I’ve been briefly introducing with the above example is the notion of process algebra (PA), where we have a set of process terms and operators for composing them, with a formal definition of both the syntax of the relevant language, built out of such basic components and operators, and of its semantics, which relates language terms to LTSs. For the sake of simplicity, I refrained from elaborating here on the mathematics of syntax and semantics definition; the interested reader is referred to the literature.
There are a lot a mathematical results behind the name PA. For instance, appropriate process algebraic relations and in particular pre-orders and equivalences have been discovered, which allow us to compare process terms w.r.t. their behaviour and, e.g., to replace a process in a model with an equivalent (but maybe cheaper to implement) one, still keeping the behaviour of the overall model unchanged (do you remember the example of the resistors R1 and R2 which, when composed in a certain way can replace a third resistor, R, thanks to a mathematical relation between the three resistors and the specific composition pattern? ... Well, we are now doing something similar, but with computer system models!!). Furthermore, in many cases, those equivalences have a textual representation, in the form of general laws, exactly as it happens in elementary algebra (thus the name of process algebra). For instance, for any processes P1, P2, P3, it holds P1 + P2 = P2 + P1 and P1 + (P2+ P3) = (P1 + P2) + P3. This means that system models expressed in PA can be manipulated, sometimes mechanically/automatically, for discovering possible design bugs (e.g. the fact that a system, after a certain behaviour hangs up, i.e. is equivalent to the zero process nil, famous because it never performs any action ...), or for simplifying designs, etc. etc.
Furthermore, a formal link can be established between system designs expressed, for instance, as PA terms and system requirements, expressed, e.g. in temporal logics, as we mentioned before. For instance, with reference to the LTS of our example above, a sentence like "In all possible runs [of a system modelled by such an LTS] whenever the system is in state s0, it will eventually reach state s4", can be formally expressed in temporal logic (although, by the way, it does not hold in our example, since any system modelled by the above LTS may keep cycling forever as follows: s0,s2, s3, s0,s2, s3, s0,s2, s3, s0,s2, s3, ....). The link between the requirement specifications and the model of a system can be implemented into software tools (typically known as model-checkers) which automatically check whether a system model satisfies a given requirement, and, if not, even yield you back a counter-example.
PA, and in general LTS based techniques, have also a strong link with standard techniques for quantitative analysis of systems, e.g. performance. This can be expressed by means of enriching PA languages with probabilistic information so that they can describe performance models, like Continuous Time Markov Chains (CTMCs), without loosing their nice compositionality features, and even serve as a formal backbone for studying fluid limit properties of system models, by mean of sophisticated PA interpretations based ordinary differential equations. These, so called Stochastic PA, are equipped with more sophisticated logics for requirements specification, which are usually obtained as appropriate extensions of temporal logics, like the Continuous Stochastic Logic (CSL), which allows us to express requirements like , e.g.,: "The probability is larger than 0.97 that a swarm of robots will reach a given target by 4 minutes". Suitable tools for automatic stochastic model-checking are available which check whether a given stochastic model, possibly expressed as a stochastic PA term, satisfies a CSL---or some other stochastic logic---formula. Finally, models written using stochastic PAs can easily be simulated using stochastic simulation techniques, or, when the models would be too huge to be simulated, the relevant results can be approximated using fluid flow, ODE based, techniques.
I’ll refrain from discussing all this now here, and I refer the interested reader to the relevant literature in the areas of concurrency theory. The above was an attempt to show that there exists indeed basic math for the design of complex computer systems; and of course there exists much more than I could mention here, which is really a fragment of the overall body of FMs. There are some people that, at this point, are still suspicious about the real “practical usefulness” of FMs and thus they are sometimes surprised by the fact that research effort and funding is devoted to the study of mathematical foundations and FMs for computer system design. Would they be as well surprised by the fact that quite some math, and related research and development, has been involved in the centuries, and is still involved, in the design of buildings, bridges, ships or aircrafts? I think they should instead be surprised by the fact that still, too often, engineers do not use FMs in SE. I would be very much surprised, and scared, if I knew that a building, a bridge, a ship, an aircraft, or a complex critical software system was not designed and implemented using the support of sound and appropriate math! And if some people are still missing some success stories on the development and use of FMs, maybe it might help them knowing that current model-checking technologies can deal with LTSs with trillions of states, and in some cases with number of states of the order of 10 power 10.000 [CAS09], and that FMs have been successfully applied to critical space applications, like the Cassini probe system (see, e.g. http://spinroot.com/spin/whatispin.html), the Mars Exploration Rovers (see the Jan. 2004 issue of COMPUTER), the Deep Space. Nomad 1 system for Antartica exploration, or the design of the Rotterdam Storm Surge Barrier which protects The Netherlands from high water and is fully automated (no man in the loop, from weather forecast to closing the barrier!), just to mention the most spectacular systems which could have not been designed without the support of FMs,and related tools, in SE. To the above, one should then add the more routine-like use of FMs in the railway sector, among others.
And then ... looking for exciting use of FMs in autonomic service component ensembles? Stay connected with the ASCENS Project web site!
[CAS09] E. Clarke, E. Emerson, and J. Sifakis. Model Checking: Algorithmic Verification and Debugging. Turing Lecture. Communications of the ACM, Vol. 52, n. 11, November 2009, pages 75—84
[Jon00] C. Jones. Thinking Tools for the Future of Computing Science. In R. Wilhelm, editor. Informatics 10 Years Back 10 Years Ahead, volume 2000 of Lectures Notes in Computer Science. Springer-Verlag, 2000. pp 112-130
[Tho00] W. Thomas. Logic for Computer Science: The Engineering Challenge. In R. Wilhelm, editor. Informatics 10 Years Back 10 Years Ahead, volume 2000 of Lectures Notes in Computer Science. Springer-Verlag, 2000. pp 257—267.
What can Formal Methods do?
In a post of F. Tiezzi to this blog, titled “Robot Swarms – What can Formal Methods do?" it has been shown that Formal Methods (FMs) can support the development of models of real (robotics) systems and that such models can be used for system simulation. It has also been (correctly!) argued that such simulation offers many advantages, especially when compared with experimentation on the real system, e.g. in terms of cost. A possible objection to Francesco’s point could be: couldn’t simulation be performed as well using models built without the use of formal modelling languages and supporting theories? In the end, this is what computer professionals have been doing for decades . . . In other words, Francesco deliberately avoided addressing the issue ‘per se’ of the role of FMs in Computer System Engineering (SE), including the engineering of complex systems of autonomic service component ensembles.
In this post I’ll try instead to focus on this very issue. The reason why I decided to do so is that my personal experience induces me to think that the role of FMs in SE is still not fully appreciated in the Computer Science (CS) community, not even in the more intellectually sophisticated part thereof, namely in the CS research community. So, I think that a few considerations on this subject might help the reader understanding also why a great deal of ASCENS effort is devoted to the development of formal modelling and analysis languages and techniques. Of course, I have to apologize with all colleagues in the area of FMs, and in particular with ASCENS friends, for inaccuracies, and incomplete or obvious statements which unavoidably will pop up in my post; on the other hand, being this the public ASCENS blog I ask knowledgeable people to tolerate my superficiality, if this can help a broader community getting a chance to appreciate the role of, and the motivations for FMs. And, ultimately, also their role in ASCENS.
My first and, I’d say major, observation is that this lack of appreciation for FMs seems to be a peculiarity of people’s attitude towards SE, not at all experienced when considering other branches of engineering. Let me start by quoting C. Jones [Jon00]: “All engineering disciplines make progress by employing mathematically based notations and methods.” Notice that the above consideration applies to all engineering disciplines, and it explicitly refers to notations and methods that are mathematically based. Is this true?
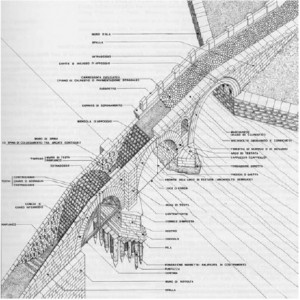
Let us consider civil engineering. In this case, graphical notations, among others, are widely used, and this goes on now for quite a long time (see the figure below [MaJ06]):
Although the result of using such graphical notations can be quite evocative, and may bear some artistic value, it is worth noting that technical drawing is regulated by rather strict rules. Such regulations are often internationally standardized and amazingly detailed (I still remember that when I was an undergraduate student, we were thought, at a technical drawing course, that when we draw a certain kind of arrows, the width of the tip should be in a fixed relationship with its length---1/3, to be precise, if I remember well!---in order for the arrow to be a “correct” one). Furthermore, we were thought specific techniques for constructing, or better, (almost) mechanically generating, “sections” of objects. Well … essentially, we were thought rigorous, sometimes formal, rules for drawing models of the artefacts we were designing, be them bridges or taps. To a certain extent, these rules were a rigorous definition of the syntax to be used for creating our models. On the other hand, the sectioning/projecting techniques were based on formal rules of mechanical manipulation of the drawings, . . . a, maybe rudimentary, form of model analysis based on formal semantics. Furthermore, in most cases, such drawings were decorated with numbers which could be used in mathematical formulas in close relation with (parts of) the drawings, or derivable from them (think, for instance, at the calculation of the max load which can safely cross a bridge, starting from the sizes, materials, and geometric relationships of the relevant components of the bridge, using the laws of statics).
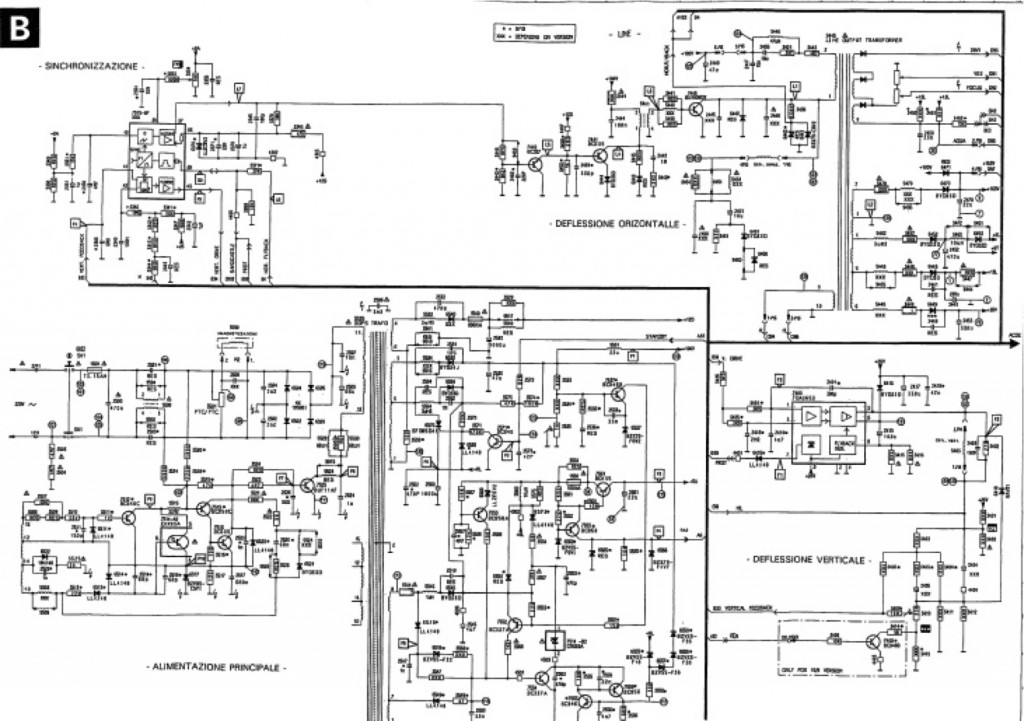
Another example of the close relationship between design notations and maths in the tradition of engineering is the design of electrical circuits. Below there is a typical (although dated!) example thereof, related to a commercial device (copyright PHILIPS):
You can see several instances of different kinds of components, connected in certain ways and with annotations, typically referring to (physical) quantities related to electricity. I want to elaborate a little bit more on electrical circuits and maths. To that purpose, let's use a simpler schema, which we all have probably got acquainted with at high school, the so-called RLC circuit.
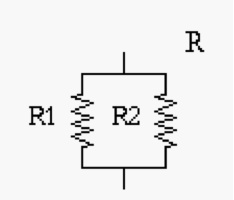
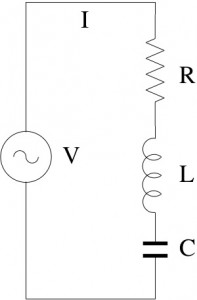We immediately note that there are some basic components (for resistors, inductances, capacitors, etc.), possibly with some quantities associated with them, and standardized systematic ways of composing them (e.g. in series, in parallel, in series-parallel, etc.). Again, although the above graphic descriptions are quite evocative of the physical objects they represent, we can use them for reasoning about our designs in rather abstract and often mechanical ways, with the help of some math, and without necessarily having to experiment repeatedly with physical realizations of our circuits. For instance, as you will remember, by using Kirchhoff laws, we can predict that the resistance offered by the circuit below at its terminals is R=R1*R2/(R1+R2).
This formal, mathematical, relationship between R, R1, R2 and the associated composition diagram allows us to replace, in any circuit, e.g. the RLC one above, a resistor of a given resistance R, say 8 Ohm, with the parallel composition of two resistors R1, R2, of, say, 16 Ohm. Notice that we can make those manipulations directly on the graphical schema, even mechanically, provided the above equality is not violated. On the other hand, the above equality comes from specific laws of physics, which are, in turn, expressed as math formulas. Although we have been using a graphical notation for circuits, I’m sure you will understand that we could describe our systems using textual notations instead, based on operators, like, say, PARALLEL(x1,s2) or SERIES (x1,x2), etc.
A closer look at the RLC circuit, and some basic knowledge of physics, allow us to express the relationships between the components of the circuit and the physical quantities of interest, e.g. the current i and voltage v at the power unit terminals (PU), at any point in time, as follows:
The solution of the above equation gives a current that changes over time with a sine like shape
The frequency w of the sine is that specific of the PU. It is useful to study how the amplitude of the above signal, i.e. the (absolute) value of the peaks, changes with w. It can be shown that (for appropriate values of R, L, and C) as w increases from 0 the amplitude increases as well, reaches a max and then decreases again, as follows:
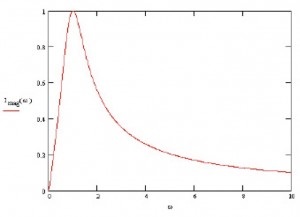The frequency corresponding the amplitude peak is the so-called resonance frequency (RF). Why is the RF so important? And, most of all, why am I bothering you with all these details? Both questions are easy to answer! The identification and study of RFs are of paramount importance in the design of systems that might be subject to oscillations (these include RLC circuits, but also bridges, ships, or aircrafts, for example); to be brief: devices and systems can be seriously damaged by too high oscillation amplitudes (bridges can crash, ships can sink or brake down...). For what concerns the second question, I used the above example for showing you that, starting from a diagram, sometimes called a blueprint, i.e. a formal syntactical description of a model of a system, and doing some manipulations of its semantics with the help of mathematics, we can characterize some peculiar features of the system we are designing. The document where the relevant peculiar features of a system are specified is the so-called technical specification, also called, in our, CS, domain, requirements specifications document. Needless to say, it is convenient that also such a document be as much rigorous as possible, even better, if it also includes some logic/mathematical formulas, as is the case for RLC systems (because this helps in having unambiguous specifications of the requirements). The process of relating a design model with the requirements specification can be seen as a process of abstraction and, of course, appropriate notions should be available also for checking that a design model satisfies a given requirement. But do we have to do all this by paper and pencil or only experimental testing? Fortunately not: we can play with software tools (see, e.g. http://ngsir.netfirms.com/englishhtm/RLC.htm), even forgetting, while designing and only to a certain extent, that behind all these activities there is a huge and solid body of mathematics supporting them, including Set Theory, Continuous Mathematics, Metric Spaces, Differential Calculus and Function Analysis, Linear Algebra, Differential Equations, just to mention a few ...
Summarizing: Civil, Naval, Nuclear, Electrical, Electronic (. . .) Engineers use notations for technical specifications (requirements specifications) as well as design specifications/models that
- are strongly based on mathematics (and physics),
- are compositional (at least in a broad sense),
- are characterized by great and flexible descriptive power,
- allow for the formal manipulation of their objects
- are heavily supported by computer (software) tools (e.g. for model analysis, including relating models to technical specs)
Society expects engineers to be aware of the underlying theories although not necessarily to be able to completely master them. I repeat it: a good, or even average, civil, electrical, etc. engineer, is socially not allowed to claim he can do without formal methods. And now: what about engineers designing complex, critical, computer/software systems? Although in the past there have been people, including respectable scientists, who have been arguing that SE is mainly a matter of art, or, at most of kraft-work, there is now some consensus, at least in the SE community itself, that it is a matter of engineering and so, as in any other branch of engineering, besides ingenuity and inspiration, there is need of systematic application of sound methodologies and techniques, with a solid mathematical basis.
But then, the question is what is the logics/mathematics basis of SE: what kind of mathematical objects, theories and techniques can best support the design activities typical of SE. I’ll touch upon these issues soon, in my next post.
[Jon00] C. Jones. Thinking Tools for the Future of Computing Science. In R. Wilhelm, editor. Informatics 10 Years Back 10 Years Ahead, volume 2000 of Lectures Notes in Computer Science. Springer-Verlag, 2000 112-130
[MaJ06] M. Mazzoleni, L. Jurina ``PONTI IN MURATURA: DIFETTI E PATOLOGIE'', CIAS 2006, Bolzano
Knowledge Representation for Autonomic Behavior
A cognitive system is considered to be a self-adaptive system that changes its behavior in response to stimuli from its execution and operational environment. Such behavior is considered autonomic and self-adaptive and is intended to drive a system in situations requiring adaptation. Any long-running system is subject to uncertainty in its execution environment due to potential changes in requirements, business conditions, available technology, etc. Thus, it is important to capture and cater for uncertainty as part of the development process. Failure to do so may result in systems that are too rigid to be fit for purpose, which is of particular concern for the domains that typically make use of self-adaptive technology, e.g., ASCENS. We hypothesize that modeling uncertainty and developing mechanisms for managing it as part of Knowledge Representation & Reasoning (KR&R) will lead to systems that are:
- more expressive of the real world;
- fault tolerant due to fluctuations in requirements and conditions being anticipated;
- flexible and able to manage dynamic changes.
Formal Approach
The ability to represent knowledge providing for autonomic behavior is an important factor in dealing with uncertainty. In our approach, the autonomic self-adapting behavior is provided by policies, events, actions, situations, and relations between policies and situations (see Definitions 1 through 8). In our KR&R model Policies (Π) are responsible for the autonomic behavior. A policy π has a goal (g), policy situations (Siπ), policy-situation relations (Rπ), and policy conditions (Nπ) mapped to policy actions (Aπ), where the evaluation of Nπ may imply the evaluation of actions (denoted with Nπ→Aπ) (see Definition 2). A condition is a Boolean function over ontology (see Definition 4) or the occurrence of specific events or situations in the system. Thus, policy conditions may be expressed with policy events. Policy situations (Siπ) are situations (see Definition 6) that may trigger a policy π, which implies the evalua-tion of the policy conditions Nπ (denoted with Siπ→π→Nπ). A policy may also comprise optional policy-situation relations (Rπ) justifying the relationships between a policy and the associated situations. The presence of probabilistic belief in those relations justifies the probability of policy execution, which may vary with time. A goal is a desirable transition from a state to another state (denoted with s⇒s') (see Definition 5). A situation is expressed with a state (s), a history of actions (Asi←) (actions executed to get to state s), actions Asi that can be performed from state s and an optional history of events Esi← that eventually occurred to get to state s (see Definition 7).
Ideally, policies are specified to handle specific situations, which may trigger the application of policies. A policy exhibits a behavior via actions generated in the environment or in the system itself. Specific conditions determine, which specific actions (among the actions associated with that policy – see Definition 2) shall be executed. These conditions are often generic and may differ from the situations triggering the policy. Thus, the behavior not only depends on the specific situations a policy is specified to handle, but also depends on additional conditions. Such conditions might be organized in a way allowing for synchroniza-tion of different situations on the same policy. When a policy is applied, it checks what particular conditions are met and performs the associated actions (see map(Nπ,Aπ) – see Definition 2). The cardinality for the policy-situation relationship is many-to-many, i.e., a situation might be associated with many policies and vice versa. Moreover, the set of policy situations (situations triggering a policy) is open-ended, i.e., new situations might be added or old might be removed from there by the system itself. With a set of policy-situation relations we may grant the system with an initial probabilistic belief (see Definition 2) that certain situations require specific policies to be applied. Runtime factors may change this probabilistic belief with time, so the most likely situations a policy is associated with can be changed. For example, the successful rate of actions execution associated with a specific situation and a policy may change such a probabilistic belief and place a specific policy higher in the "list" of associated policies, which will change the behavior of the system when a specific situation is to be handled. Note that situations are associated with a state (see Definition 7) and a policy has a goal (see Definition 2), which is considered as a transition from one state to another (see Definition 5). Hence, the policy-situation relations and the employed probabilistic beliefs may help a cognitive system what desired state to choose, based on past experience.
Case Study
To illustrate autonomic behavior based on this approach, let us suppose that we have a robot that carries items from point A to point B by using two possible routes - route one and route two (see Figure 1). A situation si1:“robot is in point A and loaded with items” will trigger a policy π1:“go to point B via route one” if the relation r(si1,π1) has the higher probabilistic belief rate (let’s assume that such a rate has been initially given to this relation because route one is shorter – see Figure 1.a). Any time when the robot gets into situation si1 it will continue applying the π1 policy until it gets into a situation si2:“route one is blocked” while applying that policy. The si2 situation will trigger a policy π2:“go back to si1 and then apply policy π3” (see Figure 1.b). Policy π3 is defined as π3:“go to point B via route two”. The unsuccessful application of policy π1 will decrease the probabilistic belief rate of relation r(si1,π1) and the eventual successful application of policy π3 will increase the probabilistic belief rate of relation r(si1,π3) (see Figure 1.b). Thus, if route one continues to be blocked in the future, the relation r(si1,π3) will get to have a higher probabilistic belief rate than the relation r(si1,π1) and the robot will change its behavior by choosing route two as a primary route (see Figure 1.c). Similarly, this situation can change in response to external stimuli, e.g., route two got blocked or a "route one is obstacle-free" message is received by the robot.
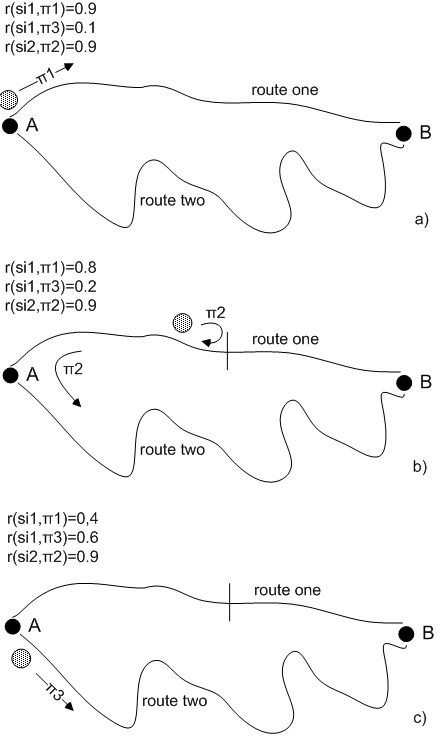
Figure 1: Self-adaptation Case Study
Knowledge Representation for ASCENS
Knowledge
When it comes to AI, we think about the knowledge we must transfer to the computerized machines and make them use that knowledge, so they become intelligent. In this regard, one of the first questions we need to answer is on the notion of knowledge. So, what is knowledge? To answer this question we should consider two facts: 1) it is known that knowledge is related to intelligence; and 2) the definition of knowledge should be given with terms from the computer domain. Scientists agree that the concept of intelligence is built upon four fundamental elements: data, information, knowledge, and wisdom. In general, data takes the form of measures and representations of the world—for example, raw facts and numbers. Information is obtained from data by assigning relevant meaning, usually by putting data in a specific context. Knowledge is a specific interpretation of information. And wisdom is the ability to apply relevant knowledge to a particular problem.
Why knowledge representation?
Intelligent system designers use knowledge representation to give computerized systems large amounts of knowledge that helps them understand the problem domain. Still computers "talk" in a "binary" language, which is simple, logical, and sound, and has no sense of ambiguity typical for a human language. Therefore, computers cannot be simply given textbooks, which they understand and use, just like humans do. Instead, the knowledge given to computers must be structured in well-founded computational structures that computer programs may translate to the binary computer language. Knowledge representation structures could be primitives such as rules, frames, semantic networks and concept maps, ontologies, and logic expressions. These primitives might be combined into more complex knowledge elements. Whatever elements they use, designers must structure the knowledge so that the system can effectively process and it and humans can easily perceive the results.
Many conventional developers doubt the utility of knowledge representation. Fact is that knowledge representation and the accompanying reasoning can significantly slow a system down when it has to decide what actions to take, and it looks up facts in a knowledge base to reason with them at runtime. This is one of the main arguments against knowledge representation. Why not simply “compile out” the entire knowledge as “procedural knowledge”, which makes the system relatively faster and more efficient. However, this strategy will work for a fixed set of tasks, i.e., procedural knowledge will give the system the entire knowledge the system needs to know. However, AI deals with an open set of tasks and those cannot be determined in advance (at least not all of them). This is the big advantage of using knowledge representation – AI needs it to solve complex problems where the operational environment is non-deterministic and a system needs to reason at runtime to find missing answers.
Knowledge Representation for ASCENS
ASCENS is an AI project tackling self-adaptation of systems operating in open-ended environment, e.g., our physical world. Such systems need to be developed with initial knowledge and learning capabilities based on knowledge processing and awareness. It is very important how the system knowledge is both structured and modelled to provide essence of awareness. We propose a special multi-tier knowledge structure, allowing for knowledge representation at different depths of knowledge.
ASCENS Knowledge Model