Knowledge Representation for Autonomic Behavior
A cognitive system is considered to be a self-adaptive system that changes its behavior in response to stimuli from its execution and operational environment. Such behavior is considered autonomic and self-adaptive and is intended to drive a system in situations requiring adaptation. Any long-running system is subject to uncertainty in its execution environment due to potential changes in requirements, business conditions, available technology, etc. Thus, it is important to capture and cater for uncertainty as part of the development process. Failure to do so may result in systems that are too rigid to be fit for purpose, which is of particular concern for the domains that typically make use of self-adaptive technology, e.g., ASCENS. We hypothesize that modeling uncertainty and developing mechanisms for managing it as part of Knowledge Representation & Reasoning (KR&R) will lead to systems that are:
- more expressive of the real world;
- fault tolerant due to fluctuations in requirements and conditions being anticipated;
- flexible and able to manage dynamic changes.
Formal Approach
The ability to represent knowledge providing for autonomic behavior is an important factor in dealing with uncertainty. In our approach, the autonomic self-adapting behavior is provided by policies, events, actions, situations, and relations between policies and situations (see Definitions 1 through 8). In our KR&R model Policies (Π) are responsible for the autonomic behavior. A policy π has a goal (g), policy situations (Siπ), policy-situation relations (Rπ), and policy conditions (Nπ) mapped to policy actions (Aπ), where the evaluation of Nπ may imply the evaluation of actions (denoted with Nπ→Aπ) (see Definition 2). A condition is a Boolean function over ontology (see Definition 4) or the occurrence of specific events or situations in the system. Thus, policy conditions may be expressed with policy events. Policy situations (Siπ) are situations (see Definition 6) that may trigger a policy π, which implies the evalua-tion of the policy conditions Nπ (denoted with Siπ→π→Nπ). A policy may also comprise optional policy-situation relations (Rπ) justifying the relationships between a policy and the associated situations. The presence of probabilistic belief in those relations justifies the probability of policy execution, which may vary with time. A goal is a desirable transition from a state to another state (denoted with s⇒s') (see Definition 5). A situation is expressed with a state (s), a history of actions (Asi←) (actions executed to get to state s), actions Asi that can be performed from state s and an optional history of events Esi← that eventually occurred to get to state s (see Definition 7).

Ideally, policies are specified to handle specific situations, which may trigger the application of policies. A policy exhibits a behavior via actions generated in the environment or in the system itself. Specific conditions determine, which specific actions (among the actions associated with that policy – see Definition 2) shall be executed. These conditions are often generic and may differ from the situations triggering the policy. Thus, the behavior not only depends on the specific situations a policy is specified to handle, but also depends on additional conditions. Such conditions might be organized in a way allowing for synchroniza-tion of different situations on the same policy. When a policy is applied, it checks what particular conditions are met and performs the associated actions (see map(Nπ,Aπ) – see Definition 2). The cardinality for the policy-situation relationship is many-to-many, i.e., a situation might be associated with many policies and vice versa. Moreover, the set of policy situations (situations triggering a policy) is open-ended, i.e., new situations might be added or old might be removed from there by the system itself. With a set of policy-situation relations we may grant the system with an initial probabilistic belief (see Definition 2) that certain situations require specific policies to be applied. Runtime factors may change this probabilistic belief with time, so the most likely situations a policy is associated with can be changed. For example, the successful rate of actions execution associated with a specific situation and a policy may change such a probabilistic belief and place a specific policy higher in the "list" of associated policies, which will change the behavior of the system when a specific situation is to be handled. Note that situations are associated with a state (see Definition 7) and a policy has a goal (see Definition 2), which is considered as a transition from one state to another (see Definition 5). Hence, the policy-situation relations and the employed probabilistic beliefs may help a cognitive system what desired state to choose, based on past experience.
Case Study
To illustrate autonomic behavior based on this approach, let us suppose that we have a robot that carries items from point A to point B by using two possible routes - route one and route two (see Figure 1). A situation si1:“robot is in point A and loaded with items” will trigger a policy π1:“go to point B via route one” if the relation r(si1,π1) has the higher probabilistic belief rate (let’s assume that such a rate has been initially given to this relation because route one is shorter – see Figure 1.a). Any time when the robot gets into situation si1 it will continue applying the π1 policy until it gets into a situation si2:“route one is blocked” while applying that policy. The si2 situation will trigger a policy π2:“go back to si1 and then apply policy π3” (see Figure 1.b). Policy π3 is defined as π3:“go to point B via route two”. The unsuccessful application of policy π1 will decrease the probabilistic belief rate of relation r(si1,π1) and the eventual successful application of policy π3 will increase the probabilistic belief rate of relation r(si1,π3) (see Figure 1.b). Thus, if route one continues to be blocked in the future, the relation r(si1,π3) will get to have a higher probabilistic belief rate than the relation r(si1,π1) and the robot will change its behavior by choosing route two as a primary route (see Figure 1.c). Similarly, this situation can change in response to external stimuli, e.g., route two got blocked or a "route one is obstacle-free" message is received by the robot.
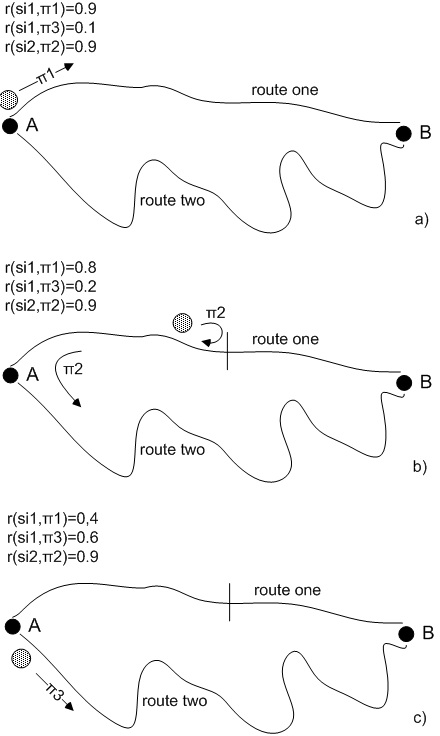
Figure 1: Self-adaptation Case Study