Engineering Distributed Adaptive Systems using Components
Traditional software engineering methodologies together with related programming paradigms have long been guiding the procedure of building software systems through the requirements and design phase to testing and deployment. In particular, engineering paradigms based on the notion of components have gained a lot of popularity as they support separation of concerns - extremely valuable when dealing with systems of high complexity.
It seems, though, that these traditional methodologies and paradigms are not sufficient when exploited in the domain of continuously changing, massively distributed and dynamic systems, such as the ones we explore in the ASCENS project. These systems need to adjust to changes in their architecture and environment seamlessly or, even better, acknowledge the absence of absolute certainty over their (constantly changing) architecture and environment. An appealing research direction seems to be the decomposition of such systems into components able to operate upon temporary and volatile information in an autonomous and self-adaptive fashion. From the software engineering perspective, two main challenges arise:
- What are the correct low-level abstractions (models, respective paradigms) that will allow for separation of concerns?
- How can we devise a systematic approach for designing such systems, exploiting the above abstractions?
In response, we propose the DEECo component model (stands for Dependable Emergent Ensembles of Components). The goal of the component model is allow for designing systems consisting of autonomous, self-aware, and adaptable components, which are implicitly organized in groups called ensembles. To this end, we propose a slightly different way of perceiving a component; i.e., as a self-aware unit of computation, relying solely on its local data that are subject to modification during the execution time. The whole communication process relies on automatic data exchange among components, entirely externalized and automated within the runtime. This way, the components have to be programmed as autonomous units, without relying on whether/how the distributed communication is performed, which makes them very robust and suitable for rapidly-changing environments.
Main Concepts
DEECo is centered around two first-class concepts: component and ensemble. These two concepts closely reflect fundamentals of the SCEL specification language. In fact, DEECo is meant to be a component model that provides software engineering constructs for SCEL concepts. Consequently, the behavior of a system of DEECo components and ensembles can be described in SCEL in a straightforward way. The two first-class DEECo concepts are in detail elaborated below:
Component
A component is an autonomous unit of deployment and computation. Similar to SCEL, it consists of:
- Knowledge
- Processes
Knowledge contains all the data and functions of the component. It is a hierarchical data structure mapping identifiers to (potentially structured) values. Values are either statically typed data or functions. Thus DEECo employs statically-typed data and functions as first-class entities. We assume pure functions without side effects.
Processes, each of them being essentially a “thread”, operate upon the knowledge of the component. A process employs a function from the knowledge of the component to perform its task. As any function is assumed to have no side effects, a process defines mapping of the knowledge to the actual parameters of the employed function (input knowledge), as well as mapping of the return value back to the knowledge (output knowledge). A process can be either periodic or triggered. A process can be triggered when its input knowledge changes or when a given condition on the component’s knowledge (guard) is satisfied.
Ensemble
Ensembles determine composition of components. Composition is flat, expressed implicitly via a dynamic involvement in an ensemble. An ensemble consists of multiple member components and a single coordinator component. The only allowed form of communication among components is communication between a member and the coordinator in an ensemble. This allows the coordinator to apply various communication policies.
Thus, an ensemble is described pair-wise, defining the couples coordinator – member. An ensemble definition consists of:
- Required interface of the coordinator and a member
- Membership function
- Mapping function
Interface is a structural prescription for a view on a part of the component’s knowledge. An interface is associated with a component’s knowledge by means of duck typing; i.e., if a component’s knowledge has the structure prescribed by an interface, then the component reifies the interface. In other words, an interface represents a partial view on the knowledge.
Membership function declaratively expresses the condition, under which two components represent the pair coordinator-member of an ensemble. The condition is defined upon the knowledge of the components. In the situation where a component satisfies the membership functions of multiple ensembles, we envision a mechanism for deciding whether all or only a subset of the candidate ensembles should be applied. Currently, we employ a simple mechanism of a partial order over the ensembles for this purpose (the “maximal” ensemble of the comparable ones is selected, the ensembles which are incomparable are applied simultaneously).
Mapping function expresses the implicit distributed communication between the coordinator and a member. It ensures that the relevant knowledge changes in one component get propagated to the other component. However, it is up to the framework when/how often the mapping function is invoked. Note that (except for component processes) the single-writer rule applies also to mapping function. We assume a separate mapping for each of the directions coordinator-member, member-coordinator.
The important idea is that the components do not know anything about ensembles (including their membership in an ensemble). They only work with their own local knowledge, which gets implicitly updated whenever the component is part of a suitable ensemble.
Example
To illustrate the above-described concepts, we’ll give an example from the Science Cloud case-study. In this scenario, several interconnected, heterogeneous network nodes (execution nodes, storage nodes) run a cloud platform, on which 3rd-party services are being executed. Moreover, the nodes can dynamically enter/leave the network. Provided an external mechanism for migrating a service from one (execution) node to another, the goal is to “cooperatively distribute the load of the overloaded (execution) nodes in the network.”
Solution in a Nutshell
Before describing the solution in DEECo concepts, we will give an outline of the final result. Basically, for the purpose of this illustration, we consider a simple solution, where each of the nodes tracks its own load and if the load is higher than a fixed threshold, it selects a set of services to be migrated out. Consequently, all the nodes with low-enough load (determined by another fixed threshold) are given information about the services selected for migration, pick some of them and migrate them in using the external migration mechanism.
The challenge here is to decide which of the nodes the service information should be given to and when, since the nodes join and leave the network dynamically. In DEECo, this is solved by describing such a node interaction declaratively, so that it can be carried out in an automated way by the runtime framework when appropriate.
Realization in DEECo
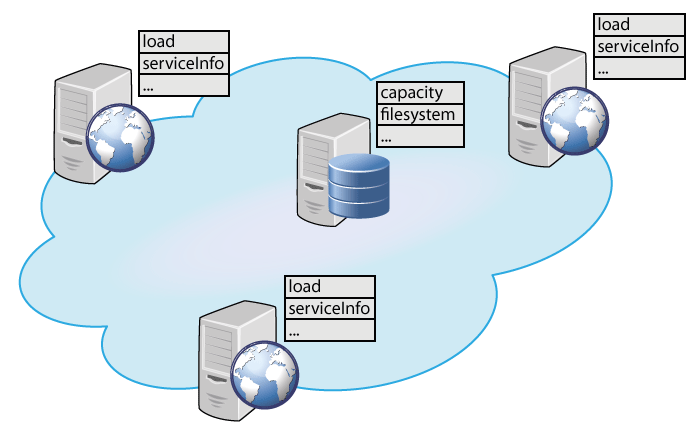
Specifically, we first identify the components in the system and their internal knowledge. In this example, the components will be all the different nodes (execution/storage nodes) running the cloud platform (Figure 1). The inherent knowledge of execution nodes is their current load, information about running services, etc. We expect an execution node component to have a process, which determines the services to be migrated in case of overload. Similarly, the inherent knowledge of the storage nodes is their current capacity, filesystem, etc.
Figure 1. Components representing the cloud nodes and their inherent knowledge.
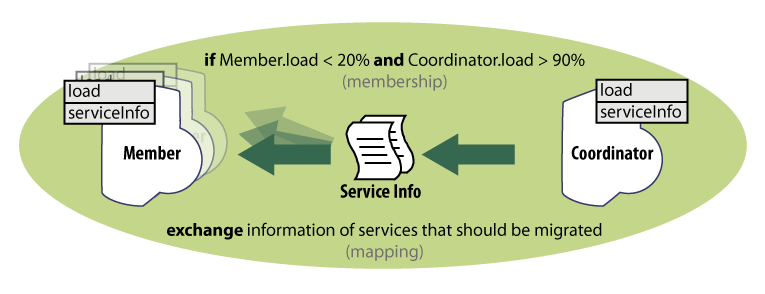
The second step is to define the actual component interaction and exchange of their knowledge. In this example, only the transfer of the information about services to be migrated from the overloaded nodes to the idle nodes is defined. The interaction is captured in a form of an ensemble definition (Figure 2), thus representing a “template” for interaction. Here, the coordinator, as well as the members, has to be an execution node providing the load and serviceInfo knowledge entries. Having such nodes, whenever the (potential) coordinator has the load above 90% and a (potential) member has the load below 20% (i.e., the membership function returns true), the ensemble is established and its mapping function is executed (possibly in a periodic manner). The mapping function in this case ensures exchanging the information about the services to be migrated from the coordinator to the members of the ensemble.
Figure 2. Definition of an ensemble that ensures exchange of the services to be migrated.
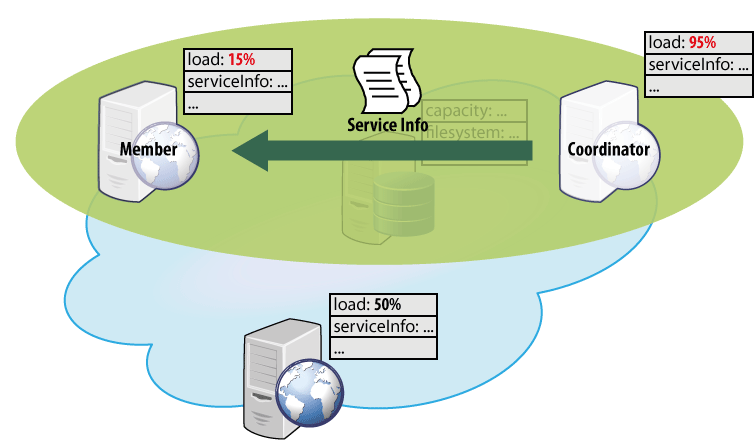
When applied to the current state of the components in the system, an ensemble - established according to the above-described definition - ensures an exchange of the service-to-be-migrated information among exactly the pairs of components meeting the membership condition of the ensemble (Figure 3).
Figure 3. Application of the ensemble definition from Figure 2 to the components from Figure 1.
According to the exchange of service information, the member nodes then individually perform service migration via the external (i.e., outside of DEECo) migration mechanism.
Current Implementation & Future Vision
As for implementation, we work on a prototype based on distributed tuple spaces and implemented in Java. The sources, as well as documentation and examples, can be found at https://github.com/d3scomp/JDEECo.
We envision that the component model outlined here will serve as the basis for a design methodology that will exploit the presented abstractions and help in building long-lasting systems of service-components and service-component ensembles.