A network-aware extension of the pi-calculus
A key aspect of modern network architectures is the possibility of manipulating the network structure at run-time. For instance, in Software Defined Networks [1] switches are instructed to install or remove forwarding rules at run-time by a controller machine; in IaaS Cloud Computing systems new nodes and links, equipped with a specific amount of storage, bandwidth, access rights..., can be allocated whenever needed.
Traditional process calculi, such as the pi-calculus, CCS and others, seem inadequate to describe these kinds of systems, because they abstract away from network details. In this post we give an overview of Network Conscious pi-calculus (NCPi) [1,2], an extension of the pi-calculus with a natural notion of network. Following [2], we will first present a core version of NCPi, closer to the pi-calculus: we will recall the basic primitives of the pi-calculus and compare them with those of NCPi. Finally, we will present the "full-fledged" calculus.
Base calculus
The pi-calculus models communication over channels. These are represented as pure names, that are entities characterized only by their identity. The novelty w.r.t. CCS is that communicated data are channels themselves, so processes can increase their communication capabilities during computation. The basic operations are output and input along channels: ab.p is a process that can send b along a and continue as p, and a(x).q can receive at a some datum that will replace x in the continuation q.
NCPi models communication over a network. There are two kinds of names: sites, atomic names of the form a representing network nodes, and links, structured names of the form lab, representing a link with name l from a to b. In addition to the same input and output primitives as the pi-calculus, NCPi also has a primitive to activate a link: lab.p is a process that can provide a transportation service over lab to the environment and continue as p.
Both calculi have operators for executing two processes p and q in parallel, written p | q, and in a non-deterministic fashion, written p + q. The parallel execution may give rise to synchronizations, when the involved processes exchange messages. The synchronization mechanism is one major difference between the pi-calculus and NCPi. Both scenarios are exemplified in the following figures, where each process is depicted as a square with tentacles to its free names (only the relevant names are shown, which we assume to occur also in the subprocesses).
Synchronization in the pi-calculus
Synchronization in NCPi
The first figure shows the synchronization of the pi-calculus processes ab.p | a(x).q on the shared channel a: this gives rise to the observation tau and results in p and q sharing the channel b. In general, the pi-calculus only allows communication on shared channels, whereas NCPi is able to model remote communications. In fact, the second figure shows two processes that do not share output and input sites, but there is a process executing in parallel that provides a link between them, thus enabling the communication. The resulting observation is the link traversed by the datum. In general, a single communication may use a chain of links of arbitrary length.
NCP inherits the mechanism for creating and communicating new resources from the pi-calculus: fresh, unguessable sites and links are declared via the restriction operator (x)p, which binds x in p; communication of bound names enlarges their scope to the receiving process, which can use such names from then on. This is the mechanism that captures mobility.
Concurrent calculus
The calculus presented so far has an interleaving semantics, meaning that the behavior of parallel processes is given by their interleaved execution. This implicitly assumes the existence of a central arbiter who decides in which order resources should be accessed. However, such assumption can be considered inadequate for distributed systems with partially asynchronous behavior. We propose a version of NCPi which is closer to "real-life" networks. Its main features are:
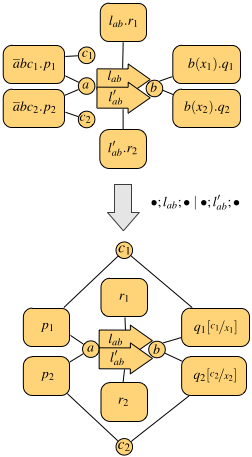
- the output operator is of the form abc.p, modeling the emission of a packet from a with destination b and payload c.
- the semantics is concurrent, in the sense that many transmissions can be observed at the same time.
Concurrency in the semantics allows the associated behavioral equivalence to distinguish a parallel process from its interleaving counterpart (technically speaking, this avoids the usual counterexample where ab.a'(x) + a'(x).ab cannot simulate ab | a'(x) whenever a is identified with a', because the two processes are not equivalent in the first place). Indeed, it can be shown that such equivalence is preserved by all NCPi operators.
An example of parallel execution is depicted in the following figure.
The top process has two links between a and b (for instance, one could be wired and the other one wireless). This enables the two processes on the left to transmit their data, both from a and addressed to b, at the same time. In fact, the resulting observation is made of two communications, each using one of the links from a to b, and both input variables are instantiated with actual values in the continuation (the bottom process).
[1] U. Montanari and M. Sammartino. Network conscious -calculus: A concurrent semantics. Electr. Notes Theor. Comput. Sci., 286:291–306, 2012. Available at http://www.di.unipi.it/ sammarti/papers/mfps28.pdf.
[2] U. Montanari and M. Sammartino. A network-conscious pi-calculus and its coalgebraic semantics. Theor. Comput. Sci. To Appear.
Analysing collective decision-making in swarm robotics
[Mieke Massink (ISTI) -- Joint work with Manuele Brambilla (ULB), Diego Latella (ISTI), Mauro Birattari (ULB) and Marco Dorigo (ULB)]
Analysing large and complex swarm robotics systems using physics-based simulations or directly with robots is often difficult and time consuming. For this reason, a common way to study these systems is by using abstract models. Models allow the developer to abstract from the complexity of a system and its implementation details and focus on the aspects that are relevant for the analysis.
An interesting problem in swarm robotics is how one can instruct robots in a swarm to make collective and optimal decisions. A further problem is then to find out whether a proposed strategy for decision making is indeed working as expected. The difficulties are caused by the fact that each robot in the swarm is on one hand operating independently from the others and on the other hand also cooperating with them and implicitly interacting with the environment creating feedback loops. Such feedback loops are known to be the cause of interesting phenomena such as that of emergent behaviour in the overall system that may sometimes be a desired effect as in the case of collective decision making.
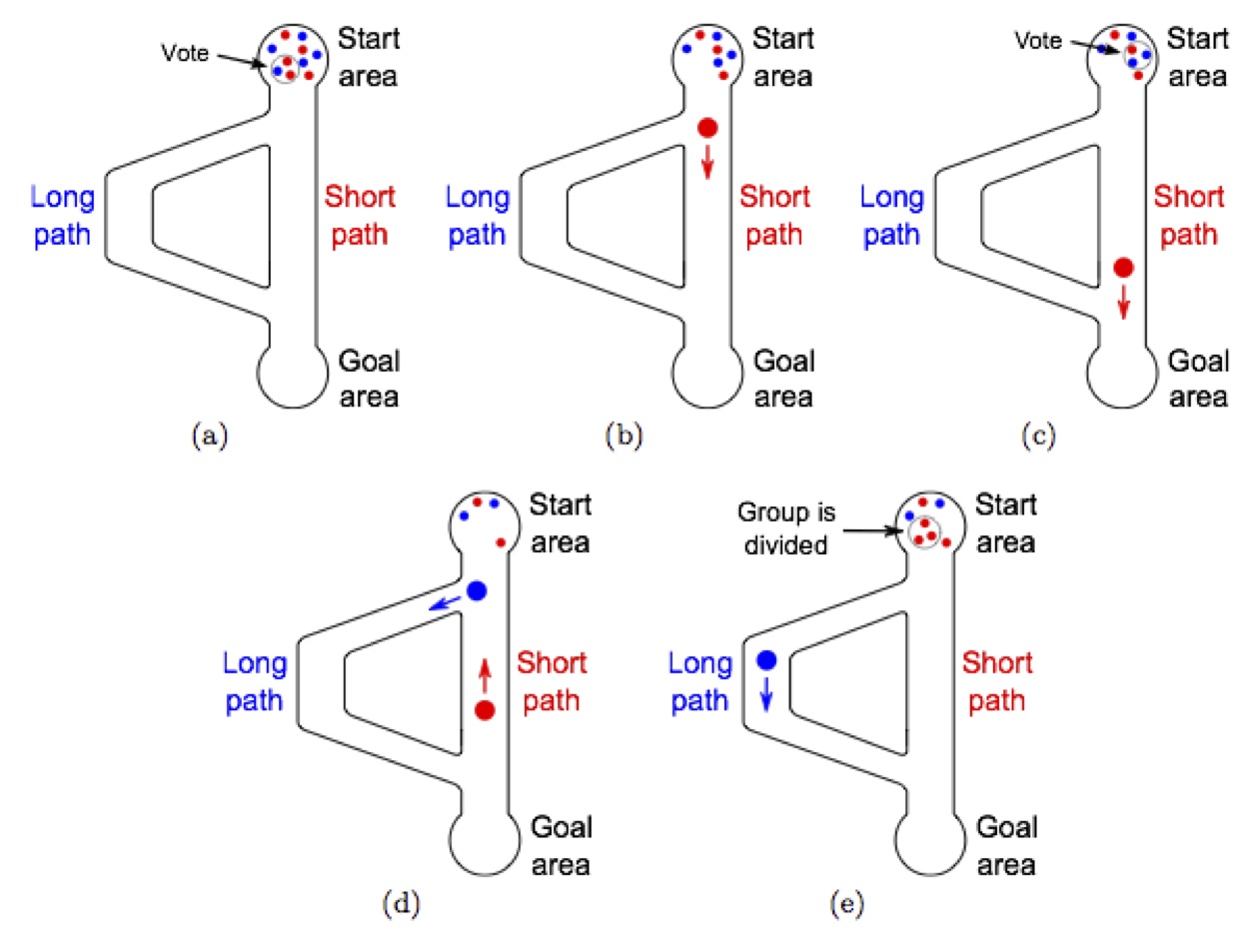
Let's have a look at a concrete example and consider a swarm of robots that need to carry objects from a start area to a goal area. To carry an object, three robots are needed that work as a team. The start and the goal areas are connected by two paths: a short path and a twice as long path. The robots have to collectively identify and choose the shortest path. They do so by a voting process based on the majority rule [1] by the members of each team. Each robot has a preferred path. When a group is formed in the start area (Figure 1(a)), a vote takes place and the group chooses the path that is preferred by the majority of the robots it is composed of (Figure 1(b)). The chosen path also becomes the new preferred path for all the robots composing the group (Figure 1(e)). For example, if two robots prefer the short path and one robot prefers the long path, the short path is chosen for the next run and the robot that preferred the long path changes its preference to the short path. Note that the voting process takes place only in the start area and no other event can change the preference of the robots. Figure 1 shows a schema of the scenario. Initially half of the swarm prefers the short path and the other half the long one.
Since the robots taking the short path spend less time out of the start area than the robots taking the long path, their participation in the vote is, on average, more frequently establishing a positive feedback on the preference to vote for the short path. This results over time in the formation of more teams preferring the short path.
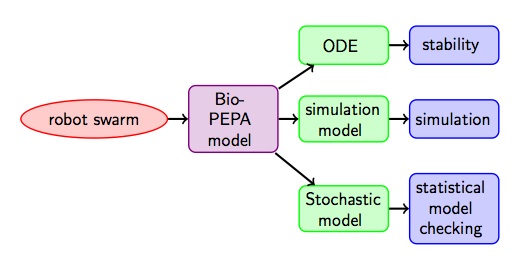
Recently, high-level modelling languages have been developed with which collective behaviour can be modelled using a population-oriented view-point. One of these languages is Bio-PEPA developed by Hillston et al. It is a variant of stochastic process algebra and therefore has important and useful properties such as compositionality: the overall system can be built from smaller basic components. But at least as important, different mathematical models can be derived from a Bio-PEPA specification that can be used in particular to analyse systems with a very large number of components applying analysis techniques such as stochastic simulation, statistical model checking and fluid flow analysis (see Fig. 2). The latter is a method that approximates, in a deterministic way, via differential equations, the change over time of the number of objects that are in a particular state. In our case for example the number of robots that prefer the short path.
This combination of a high-level language and sophisticated scalable analysis techniques makes it possible to analyse also swarms of large dimensions in an efficient way.
The idea of statistical model checking is to generate random executions of the system model and check whether they satisfy a particular property of interest (see Fig. 3). Statistical methods are then applied on the outcomes of those checks.
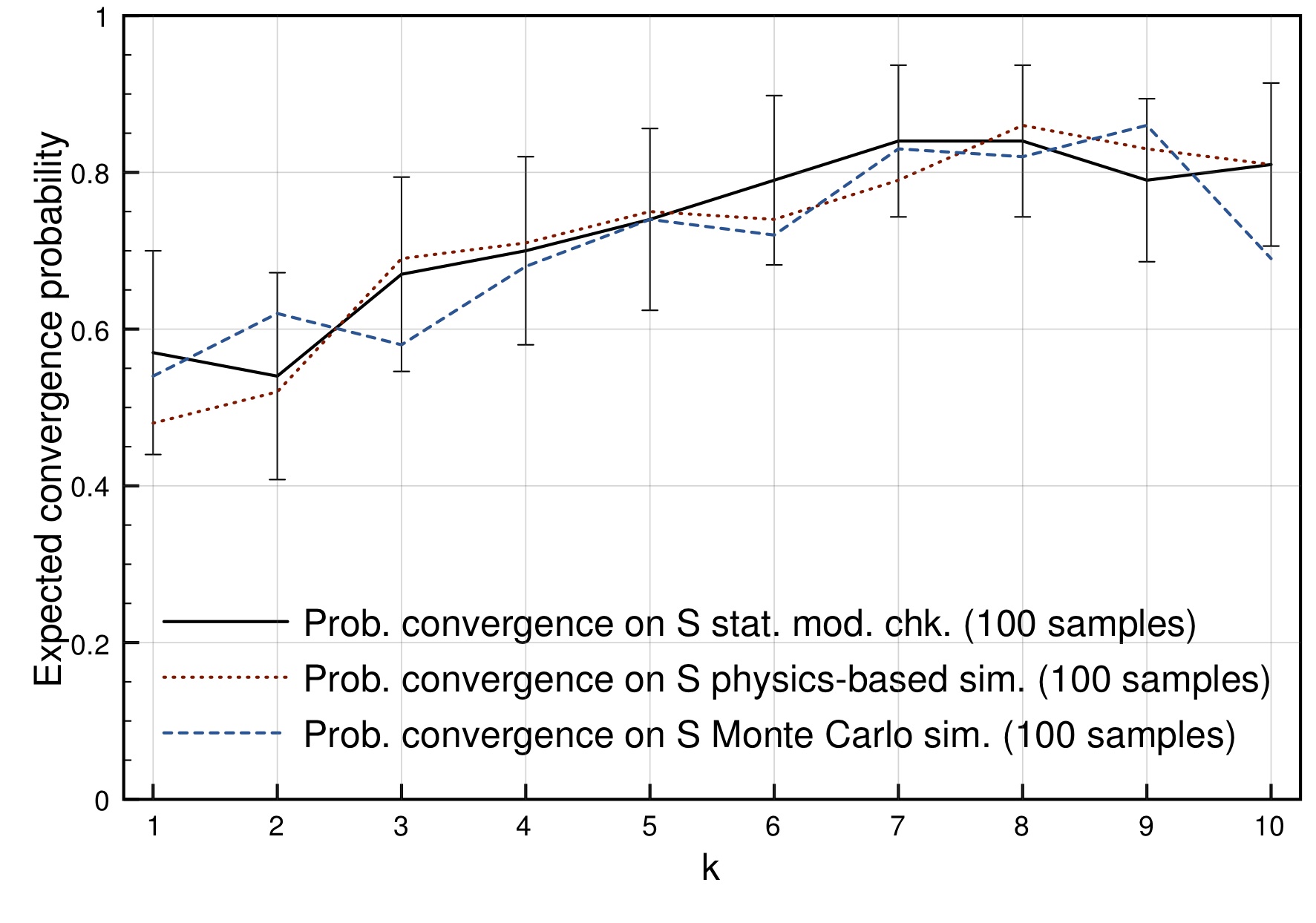
For example, we can then automatically check what is the probability that the swarm reaches a decision and, if so, what is the probability that it is the desired decision. In Fig. 4 below the probability of convergence on the shortest path is shown for different average numbers of active teams k (and thus different numbers of robots that are in the start area at any time). For a swarm of 32 robots and with one path twice as long as the other the best probability is reached when there are on average about eight teams active. The results obtained with statistical model checking are comparable with those obtained via more common swarm robotics analysis methods such as physics-based simulation, but require much less time to be performed.
What is even more of interest is that starting from a high-level language as Bio-PEPA it is easy to check what happens with the system under different circumstances. For example, what would happen if in the beginning the preferences for the different paths were not equally distributed among the robots in the start area. Or what would happen if most of the time almost all robots are away from the start area and the composition of teams could get easily biased or vary a lot due to the small number of robots from which a team would be selected. Or what would happen if some percentage of the robots would refuse to adjust their preference to comply with the majority.
Fluid flow analysis of the same model may provide a computationally efficient way to get insight in the average behaviour of the swarm for very large populations. In Fig. 5 we see results for a swarm composed of 32,000 robots, all initially in the start area and then, when time passes many robots in the swarm leave this area and after a short while robots in favour of the short path S are increasingly dominating the population. The figure shows that the results of stochastic simulation (G1) of the whole system and the fluid (ODE) analysis are showing good correspondence, but the latter results are much faster to obtain and are insensitive to the actual size of the population.
A further research challenge will focus on analysing the effectiveness of decision strategies that can dynamically adapt to changing circumstances such as new shorter paths being created or optimal paths getting inaccessible.
References for further reading:
[1] M. A. Montes de Oca, E. Ferrante, A. Scheidler, C. Pinciroli, M. Birattari, and M. Dorigo. Majority-rule opinion dynamics with differential latency:
A mechanism for self-organized collective decision-making. Swarm Intelligence, 5(3-4):305-327, 2011.
[2] M. Massink, M. Brambilla, D. Latella, M. Dorigo, and M. Birattari. Analysing
robot swarm decision-making with Bio-PEPA. In Swarm Intelligence,
volume 7461 of Lecture Notes in Computer Science, pages 25-36. Springer,
Heidelberg, 2012.
[3] M. Massink, M. Brambilla, D. Latella, M. Dorigo, and M. Birattari. On the use of Bio-PEPA for Modelling and Analysing Collective Behaviours in Swarm Robotics. Swarm Intelligence, April 2013.