Statistical Model-Checking

Computer systems play a central role in modern societies and their errors can have dramatic consequences. For example, such errors could jeopardize a banking system, possibly stalling the economy of a whole country or, more dramatically, endanger human life through the failure of some safety critical systems (railway signing, integrated avionics, air-traffic, medical life support machines, automotive electronics). It is therefore not surprising that proving the correctness of computer systems is a highly relevant problem. Unfortunately, the growing complexity in system design makes it almost impossible to ensure correctness simply by looking at the (possibly distributed) code. Automatic techniques are thus needed.

The most common method to ensure the correctness of a system is testing (see [3] for a survey). After the computer system is  constructed, it is tested using a number of test cases with predicted outcomes. Testing techniques have shown effectiveness in bug hunting in many industrial applications. Unfortunately, testing is not a panacea. Indeed, since there is, in general, no way for a finite set of test cases to cover all possible scenarios, errors may remain undetected. There are also methods that can ensure the full correctness of a system. Those methods, also called formal methods, use mathematical techniques to check whether the system will behave correctly for all possible scenarios. Over the past, formal methods such as symbolic model checking [13] have been used to verify systems with more than 10^20 reachable states [4].

In an ideal world, it would thus be ``better'' to use formal methods rather than testing. Unfortunately, improvements in the development of formal methods do not seem to follow the increasing complexity in system design. Nowadays, most of formal methods suffer from the so-called state-space explosion problem, which makes them unusable for large industrial size applications. As testing does not suffer from the same problem, it remains the only scalable technique and is thus the one promoted by the industrials.

 

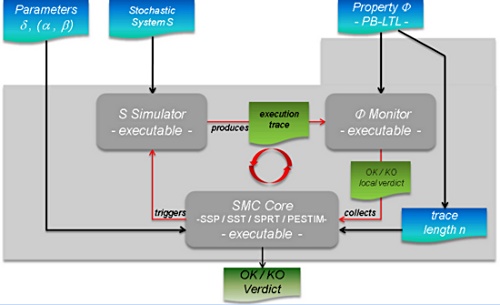
As we already said, the major drawback with testing is that, in general, it does not give any confidence on the correctness of the entire system. This lack of accuracy has motivated the development of new algorithms that combine testing techniques with algorithms coming from the statistical area. Those techniques, also called Statistical Model Checking techniques (SMC) [9, 15], can be seen as a trade-off between testing and formal verification. In fact, SMC is very similar to Monte Carlo used in industry, but it relies on a formal model of the system. The core idea of SMC is to monitor a number of simulations of a system whose behaviors depend on a stochastic semantic. Then, one uses the results of statistics (e.g. sequential hypothesis testing or Monte Carlo) together with the simulations to get an overall estimate of the probability that the system will behave in some manner. While the idea resembles the one of classical Monte Carlo simulation, it is based on a formal semantic of systems that allows us to reason on very complex behavioral properties of systems (hence the terminology). This includes classical reachability property such as ``can I reach such a state ?'', but also non trivial properties such as ``can I reach this state x times in less than y units of time ?''. Of course, in contrast with an exhaustive approach, such a simulation-based solution does not guarantee a result with 100% confidence. However, it is possible to bound the probability of making an error. Simulation-based methods are known to be far less memory and time intensive than exhaustive ones, and are sometimes the only option [10].

Statistical model checking is widely accepted in various research areas such as software engineering, in particular for industrial applications [1, 12, 7], or even for solving problems originating from systems biology [6, 11]. There are several reasons for this success. First, SMC is very simple to understand, implement, and use. Second, it does not require extra modeling or specification effort, but simply an operational model of the system that can be simulated and checked against state-based properties. Third, it allows us to verify properties [5, 1] that cannot be expressed in classical temporal logics. Finally, SMC allows to approximate undecidable problems. This latter observation is crucial. Indeed most of emerging problems such as energy consumption are undecidable [8, 2] and can hence only be estimated.

Saddek Bensalem
Verimag

[1] Ananda Basu, Saddek Bensalem, Marius Bozga, Benoit Caillaud, Benoit Delahaye, Axel Legay. Statistical Abstraction and Model-Checking of Large Heterogeneous Systems. In FMOODS/FORTE, 2010.

[2] P. Bouyer, U. Fahrenberg, K. G. Larsen, and N. Markey. Timed automata with observers under energy constraints. In HSCC, pages 61-70. ACM ACM, 2010.

[3] M. Broy, B. Jonsson, J.-P. Katoen, M. Leucker, and A. Pretschner, editors. Model-Based Testing of Reactive Systems, Advanced Lectures The volume is the outcome of a research seminar that was held in Schloss Dagstuhl in January 2004, volume 3472 of Lecture Notes in Computer Science. Springer, 2005.

[4] J. R. Burch, E. M. Clarke, K. L. McMillan, D. L. Dill, and L. J. Hwang. Symbolic model checking : 1020 states and beyond. Information and Computation, 98(2) :142-170, 1992.

[5] E. M. Clarke, A. Donzé, and A. Legay. Statistical model checking of mixed-analog circuits with an application to a third order delta-sigma modulator. In Proc. of 3rd Haifa Verification Conference (HVC), volume 5394 of LNCS, pages 149-163. Springer, 2008.

[6] E. M. Clarke, J. R. Faeder, C. J. Langmead, L. A. Harris, S. K. Jha, and A. Legay. Statistical model checking in biolab : Applications to the automated analysis of t-cell receptor signaling pathway. In CMSB, volume 5307 of LNCS, pages 231-250. Springer, 2008.

[7] E. M. Clarke and P. Zuliani. Statistical model checking for cyber-physical systems. In ATVA, volume 6996 of Lecture Notes in Computer Science, pages 1-12. Springer, 2011.

[8] U. Fahrenberg, L. Juhl, K. G. Larsen, and J. Srba. Energy games in multiweighted automata. In ICTAC, volume 6916 of Lecture Notes in Computer Science, pages 95-115. Springer, 2011.

[9] T. Hérault, R. Lassaigne, F. Magniette, and S. Peyronnet. Approximate probabilistic model checking. In Proc. of 5th Int. Conference on Verification, Model Checking, and Abstract Interpretation (VMCAI), volume 2937 of LNCS, pages 73-84. Springer, 2004.

[10] D. N. Jansen, J.-P. Katoen, M.Oldenkamp, M. Stoelinga, and I. S. Zapreev. How fast and fat is your probabilistic model checker? an experimental performance comparison. In HVC, volume 4899 of LNCS. Springer, 2007.

[11] S. K. Jha, E. M. Clarke, C. J. Langmead, A. Legay, A. Platzer, and P. Zuliani. A bayesian approach to model checking biological systems. In Proc. 7th Int. Computational Methods in Systems Biology, 7th Int. conference (CMSB), volume 5688 of LNCS, pages 218-234. Springer, 2009.

[12] J. Martins, A. Platzer, and J. Leite. Statistical model checking for distributed probabilistic-control hybrid automata with smart grid applications. In ICFEM, volume 6991 of Lecture Notes in Computer Science, pages 131-146. Springer, 2011.

[13] K. McMillan. Symbolic Model Checking. PhD thesis, Carnegie Mellon University,
1993.

[14] K. Sen, M. Viswanathan, and G. Agha. Statistical model checking of black-box probabilistic systems. In Proc. of 16th Int. Conference on Computer Aided Verication (CAV), LNCS 3114, pages 202-215. Springer, 2004.

[15] H. L. S. Younes. Verication and Planning for Stochastic Processes with Asynchronous Events. PhD thesis, Carnegie Mellon, 2005.