Global Parking Allocation
The e-Mobility case study aims at solving global problems, involving large ensembles of different vehicles. Such large problems tend to be complex to solve and often a globally optimal solution may be impossible to find. For this reason specific strategies are needed to solve them. In particular, we are interested in the parking optimization problem, consisting in finding the best parking lot for each vehicle of an ensemble. The best parking lot is chosen by considering: the distance from the current location of the vehicle to the parking lot, the distance from the parking lot to the appointment location and the cost of the parking lot.
We present two approaches to solving the parking optimization problem, joint work between Ugo Montanari, Giacoma Valentina Monreale and Matteo Sammartino at the University of Pisa, and Nicklas Hoch, at Volkswagen AG, Corporate Research Group in Wolfsburg. These approaches are based on the coordination of declarative and procedural knowledge. Declarative knowledge consists in a global description of the problem and its structure, in terms of its subproblems. General algorithms can be applied at this level, with high computational cost. Procedural knowledge defines which strategies should be applied to subproblems, and how their solutions can be combined into a possibly suboptimal, but acceptable global solution. Strategies are often more efficient than general algorithms, because they rely on specific knowledge about problems, which could also allow for the application of heuristics in order to improve the computational cost.
Both approaches are based on the representation of optimization problems as Soft Constraint Satisfaction Problems (SCSPs) [1], that are Constraint Satisfaction Problems where constraints are soft, meaning that they are preferred, but not required to be satisfied. Preference is formalized as a cost associated to each assignment of constraint variables. Optimality is defined in terms of the overall cost, which should be typically minimized.
Soft Constraint Logic Programming
The first approach consists in decomposing the global optimization problem in many local optimization problems, one for each vehicle of the ensemble, consisting in determining the best parking lot for it. All these local problems are solved separately by using an implementation of Soft Contraint Logic Programming (SCLP) [2]. The orchestrator implementing the coordination strategy then receives the results of all the local optimization solutions and checks if the local solutions all together form an admissible global solution, i.e., if no parking lot receives a number of cars larger than its capacity. If it is so, the problem is solved, otherwise the orchestrator queries the declarative knowledge again, but now by increasing the costs of the parking lots which received too many requests. The procedure is repeated, with suitable variations, until a global solution is found. Notice that in this way the orchestrator has a hypothetical, transactional behavior, with the options of committing (a solution is found) or partially backtracking (on the parkings which are overfull). The solution is guaranteed to be just an acceptable global solution: it may or may not be globally optimal. However, sub-optimality is in general needed to solve the problem in reasonable time.
The choice of SCLP is justified by its flexibility and expressiveness. On the one hand, the programmer could easily use SCLP to experiment on various optimization strategies for this and other more complex problems for electric vehicles. On the other hand, the interaction between the local optimizer and the global orchestrator is easier if the latter is declarative as it is the case for SCLP.
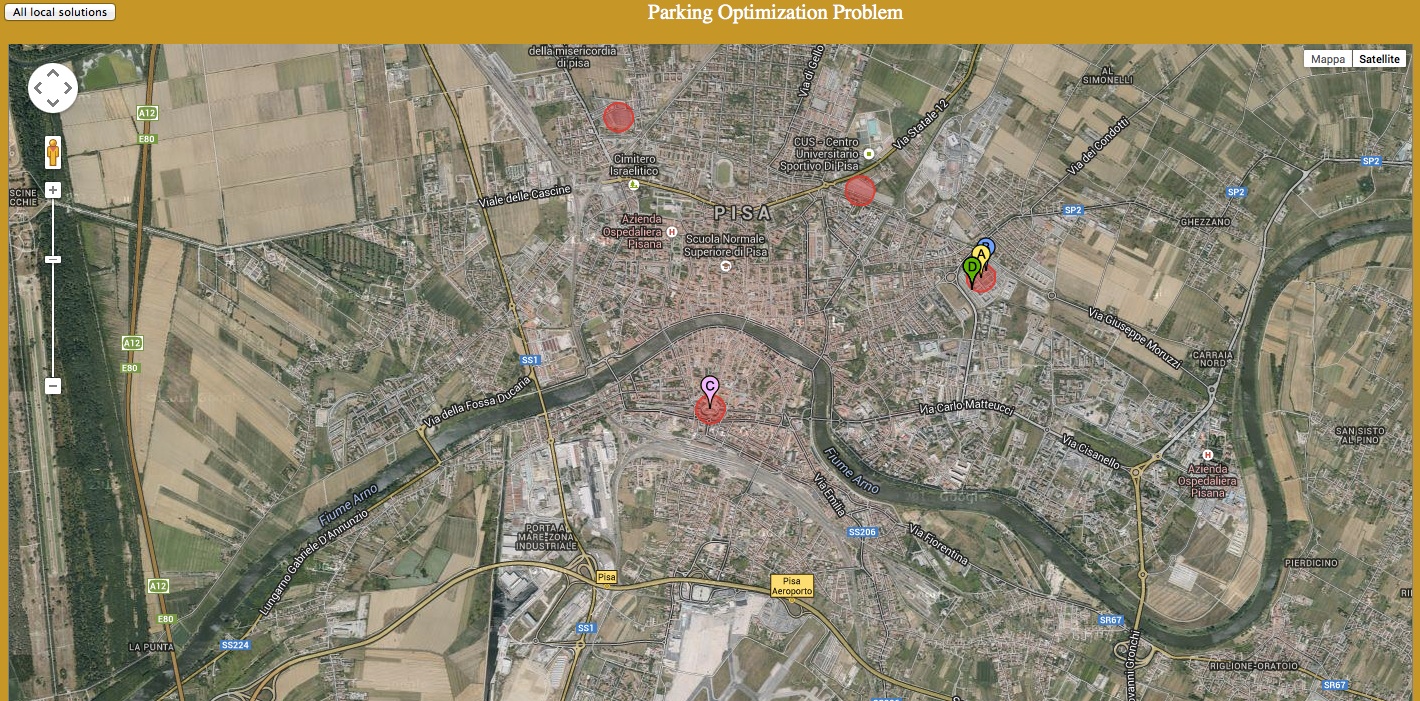
The coordination technique has been implemented in a demo application. We used Java for the orchestrator and CIAO [3] to model and solve the local problems. The figure below shows one phase of this execution.
There, four vehicles, represented by the markers A, B, C and D are finding a parking lot. Parking lots are represented by circles and each has a capacity of two vehicles. Each vehicle has autonomously computed the best parking lot for it and has sent its local solution to the Java orchestrator. Therefore, the vehicles A, B and D would like to park in the rightmost parking lot, while C prefers the parking lot at the lower part of the map. The orchestrator checks if each parking lot is able to satisfy the requests of the vehicles. In this case, since there are too many requests for the rightmost parking lot, the orchestrator increases the cost of it and asks the vehicles to recompute new local solutions.
Details about SCLP approaches to e-mobility optimization problems in ASCENS can be found in [5,6].
An algebraic approach to SCSPs
The second approach consists in representing SCSPs as terms of an algebraic specification, similar to a process calculus. These terms are then inductively evaluated in a domain of cost functions, where operators are interpreted as optimization steps. Using a dynamic programming approach, optimization is then carried out on these functions. The crucial point is that syntax also determines the variable elimination strategy, i.e., a solution to the secondary optimization problem of dynamic programming.
In order to illustrate this approach in more detail, we consider the term
(x1)(x2)(x3) ( A(x1,x3) ‖ B(x2,x3) ‖ C(x2) )
It represents a system with three parking zones A,B and C. Variables represent vehicles, and atomic terms A(x1,x3), B(x2,x3), C(x3) tell which vehicle can be parked in each zone. Each restricted variable must be parked in one of the zones within its scope.
Each zone comes with two pieces of information: a capacity and a function telling the cost of parking vehicles inside the zone. This allows us to give cost functions for each atomic subterm, and to inductively construct functions for complex terms. Restrictions is interpreted as variable elimination: the cost function in its scope should be optimized w.r.t. the restricted variable. Therefore, the position of restrictions determines a solution for the secondary optimization problem.
In the term shown above, restrictions are all outside (we say that the term is in normal form), meaning that we optimize w.r.t. all variables at once. This is inefficient, because it is clear that x1 must be parked inside A and x2 inside either B or C. Therefore, we introduce a scope extension axiom that allows restrictions to be moved. The following term
(x3)( (x1)A(x1,x3) ‖ (x2)( B(x2,x3) ‖ C(x2) ) )
is said to be in canonical form (namely no restriction can be pushed inside further) and describes a more efficient solution for the secondary optimization problem.
Given a SCSP term p, an essential property is that its cost function can be represented as a finite table, because only assignments to free variables of p matter. This allows computing cost functions using dynamic programming with tabling. More precisely, one can proceed in a bottom-up style, from atomic subterms to increasingly complex terms; tabular representations of cost functions are computed the first time they are encountered, once and for all.
An example is shown in the following figure, where double square brackets denote the evaluation operation that gives cost functions for terms. Tables (a)-(c) show cost functions for each zone. Actual cost entries are arbitrary. The leftmost columns indicates whether a car is parked inside (✓) or outside (-) the subsystem described by the term.
The resolution algorithm eliminates all the variables in the order they appear, from the inmost to the outmost one. It has the following steps:
- Elimination of x1: Table (d) is computed by forcing x1 to be inside A;
- Elimination of x2: Table (e) is computed by taking the best parking option for x2, i.e., the one that minimizes the total cost, for each possible value of x3;
- Elimination of x3: Table (f) is computed by taking the best parking option for x3.
Tracking back through the tables, we find the optimal variable assignment, namely: x1 and x3 inside A, with cost 3 and 4 respectively; x2 inside C, with cost 1.
Exploiting specific knowledge about the parking system, and the applicative scenario it is part of, we can apply some heuristics in order to reduce the complexity of the problem, possibly at the cost of having sub-optimal, but hopefully still acceptable, solutions. A few options are:
- Restrict the number of possible zones for each car. Keeping only some of the best parking options for each car makes the solution simpler. However, it may increase the total cost (and it may even make the solution impossible).
- Hierarchical organization of zones. Similar zones could be merged, leading to a smaller term. The hierarchy could depend on particular events such as soccer games, theater shows, etc.
- Bound size for tables. We could impose a maximum size for dynamic programming tables. Bigger tables could be replaced by some smaller ones, taking some averages (see [4]). The advantage is a lower storage cost and lower computational complexity of term evaluations.
Details and full proofs can be found in [7].
References
[1] Rossi, F., van Beek, P., Walsh, T.: Handbook of Constraint Programming (Foundations of Artificial Intelligence). Elsevier Science Inc. (2006)
[2] Bistarelli, S., Montanari, U., Rossi, F.: Semiring-based contstraint logic programming: syntax and semantics. ACM Trans. Program. Lang. Syst. 23(1), 1–29 (2001)
[3] Bueno, F., Cabeza, D., Carro, M., Hermenegildo, M.V., Lopez-Garcia, P., Puebla, G.: The ciao prolog system. Reference manual. Tech. Rep. CLIP3/97.1, School of Computer Science, Technical University of Madrid (UPM) (1997)
[4] Montanari U.: On the optimal approximation of discrete functions with low-dimensional tables. IFIP Congress (1971)
[5] Bures, T.,De Nicola, R., Gerostathopoulos, I., Hoch, N., Kit, M., Koch, N., Monreale, G.V., Montanari, U., Pugliese, R., Serbedzija, N., Wirsing, M., Zambonelli, F.: A Life Cycle for the Development of Autonomic Systems: The E-mobility Showcase. In: SASO, Awareness Workshop (2013)
[6] Monreale, G.V., Montanari, U., Hoch, N.: Soft constraint logic programming for electric vehicle travel optimization. In: 26th Workshop on Logic Programming (2012)
[7] Hoch, N., Monreale, V., Montanari, U., Sammartino, M.: Declarative vs procedural approach for scsp with an application to an e-mobility optimization problem (2014), Internal Report